تفاوت نرخ مؤثر و نرخ اسمی

احتمالا شما هم شنیده‌اید که بانک‌ها، تسهیلاتی با نرخ سود 18 درصد اعطا می‌کنند؛ اما این نرخ 18 درصد به چه معناست؟

نرخ سود اسمی (سود بانکی)

در ادبیات مالی، این نرخ سود را با نام نرخ سود اسمی[1] معرفی می‌کنند. نرخ سود اسمی نشان‌ دهنده نرخ سود سالانه‌ای است که وام‌گیرنده بدون در نظر گرفتن تعداد دوره‌های مرکب شدن سود (تعداد دوره‌های محاسبه سود) پرداخت می‌کند.

منظور از تعداد دفعات مرکب شدن سود، تعداد دفعاتی است که سود حاصل از بخش تسویه نشده یک وام محاسبه می‌شود. مثلا در مورد وام‌هایی که اقساط آن‌ها ماهانه پرداخت می‌شود، تعداد دفعات محاسبه سود در سال برابر با 12 است و یا برای سپرده‌هایی که به صورت روزشمار سود می‌دهند تعداد دفعات مرکب شدن سود (تعداد دفعات محاسبه سود) در سال برابر با 365 است.

برای مثال، دو وام با مبلغ 1,000,000,000 تومان و نرخ سود 18 درصد را در نظر بگیرید. نرخ سود وام اول به صورت ماهانه و وام دوم به صورت روزانه محاسبه می‌شود. برای سهولت فرض کنید که بازپرداخت هر دو وام پس از یکسال و به صورت یکجا انجام می‌شود. می‌خواهیم مقدار بازپرداخت هر یک از این وام‌ها را محاسبه کنیم:

مقدار بازپرداخت وام اول:

مقدار بازپرداخت وام دوم:

همانطور که مشاهده می‌کنید اگر چه نرخ اعلام شده از سوی بانک برای هر دو وام یکسان است؛ اما تفاوت در تعداد دوره‌های مرکب شدن سود (محاسبه سود)، باعث شده که مبلغ بازپرداخت آن‌ها با یکدیگر متفاوت باشد. بنابراین، استفاده از نرخ اسمی برای مقایسه وام‌ها با یکدیگر راه مناسبی نیست.

نرخ سود مؤثر

برای حل این مشکل، در ادبیات مالی نرخ دیگری تحت عنوان نرخ سود مؤثر سالانه[2] معرفی شده است. نرخ موثر را می‌توان به صورت نرخ واقعی بازده سالانه‌ تعریف کرد که یک سپرده‌گذار یا وام‌دهنده با در نظر گرفتن تعداد دوره‌های مرکب شدن در سال پرداخت یا دریافت می‌کند. برای محاسبه نرخ سود موثر سالانه می‌توان از معادله زیر استفاده کرد:

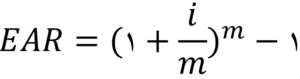
در این معادله، i نشان‌ دهنده نرخ سود اسمی سالانه و m تعداد دفعات مرکب شدن سود در سال است. از این معادله می‌توان دریافت که هر چه تعداد دفعات مرکب شدن سود و نرخ سود اسمی بیشتر باشد، نرخ سود موثر سالانه نیز بیشتر خواهد بود.

حال می‌توانیم نرخ سود موثر سالانه را برای دو وام قبلی خود محاسبه کنیم:

نرخ موثر وام اول:

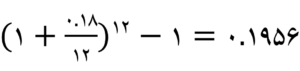
نرخ موثر وام دوم:

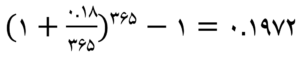
همان طور که قابل مشاهده است اگر چه هر دو وام نرخ اسمی یکسانی دارند، اما نرخ موثر وام دوم که سود آن به صورت روزانه محاسبه می‌شود بیشتر است.

از مطالب فوق می‌توان نتیجه گرفت که برای مقایسه دو وام، باید به تعداد دفعات مرکب شدن نرخ سود توجه کرد و نرخ سود موثر سالانه را مبنا قرار داد؛ زیرا در یک دوره زمانی مشخص، مبلغ پرداختی یا سود دریافتی وامی بیشتر است که نرخ موثر بالاتری داشته باشد.

[1] Nominal interest rate

[2] Effective annual interest rate (EAR)